| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- utilty type
- 리액트
- CSS
- JS console
- returnType
- Chart.js
- 타입스크립트
- 타입좁히기
- javascript
- React.js
- 제네릭
- 성능최적화
- const 단언문
- NonNullable
- 레이아웃쪼개기
- 반복줄이기
- vue.js
- typescript
- 커스텀
- 개발콘텐츠
- 티스토리꾸미기
- reactjs
- 폰트적용하기
- 2022
- React Native
- click and drag
- 누구나 자료구조와 알고리즘
- TSDoc
- 공통컴포넌트
- react
- Today
- Total
몽땅뚝딱 개발자
📔 [스터디] 학습노트 - 시간복잡도 본문

시간 복잡도란?
◽️ 특정한 크기의 입력에 대하여 알고리즘의 수행 시간을 분석하는 방법이다.
◽️ 일반적으로 알고리즘 성능을 나타내는 척도 중 하나로, 보통 성능(performance)은 실행 시간(time)과 메모리(memory) 용량으로 평가된다.
◽️ 알고리즘 같은 경우는 메모리를 적게 사용하면서 알고리즘의 수행 시간이 빠른 것이 좋은 알고리즘이라고 한다.
◽️ 동일한 기능을 수행하는 알고리즘들이 있다면, 이들 사이에서 복잡도가 낮을수록 성능이 우수하다.
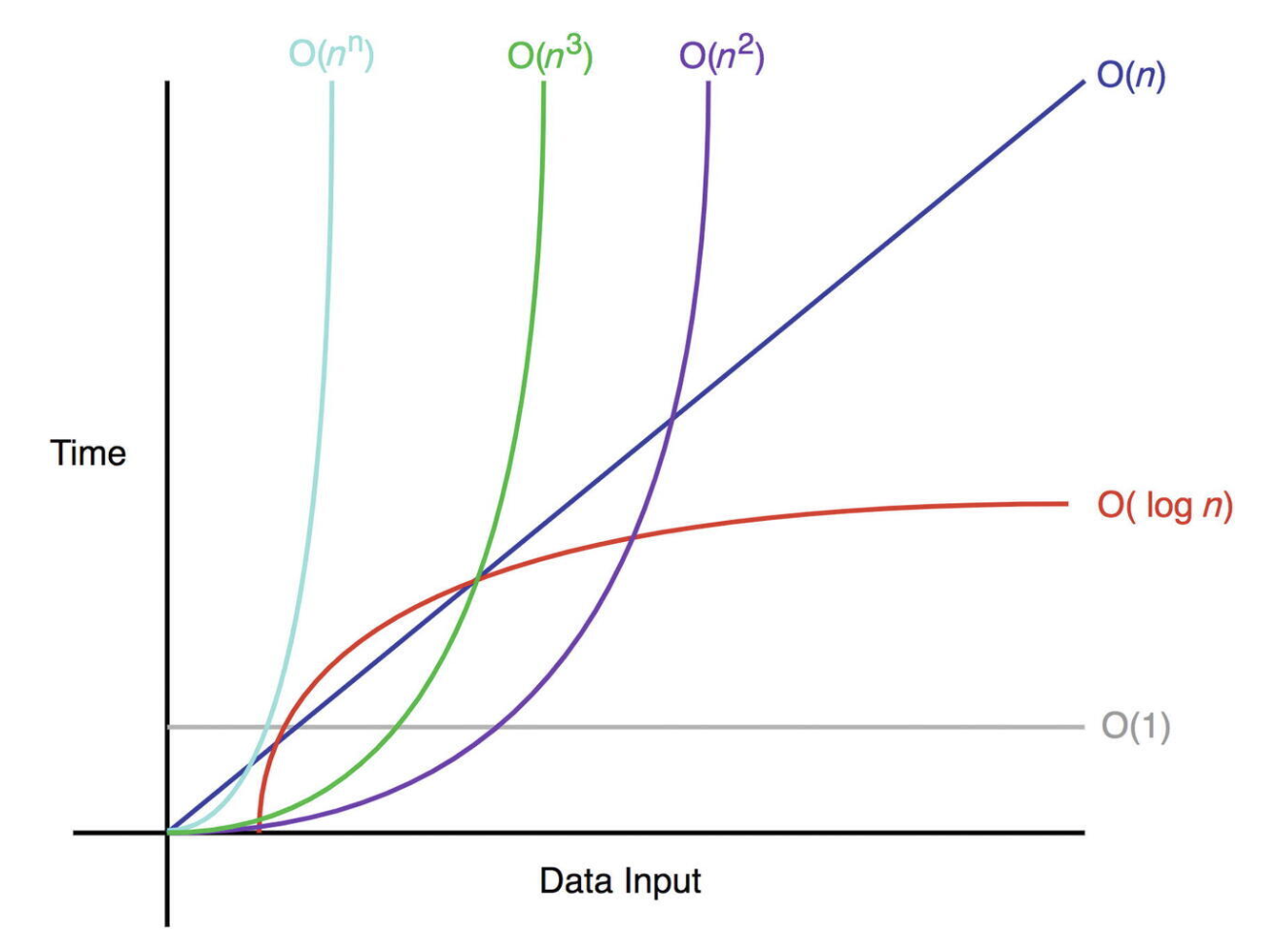
빅 오 표기법
1) 개념
"데이터 원소가 N개일 때 알고리즘에 몇 단계가 필요할까?"
알고리즘의 시간복잡도를 수학적 개념을 차용하여 형식화한 표현을 '빅오 표기법'이라고 한다. 이 표기법을 사용하여 주어진 알고리즘의 효율성을 쉽게 분류하고 이해시킬 수 있다.
- O(N)
◽️ "빅 오 N"이라고 발음하며 "차수 N"이라고도 부른다.
◽️ "알고리즘에 N단계가 필요하다"라는 뜻이다.
◽️ 이 O(N)인 알고리즘을 선형 시간을 갖는 알고리즘이라고도 부른다.
◽️ N이 얼마든 항상 상수 단계만 필요하기떄문에 상수 시간(constant time)을 갖는 알고리즘이라고도 표현한다.
◽️ 원하는 값을 찾을 때 까지 왼쪽에서 오른쪽으로 한 번에 한 셀씩 확인하는 선형검색이 대표적인 예시이다.
const arr = [1, 2, 3] arr.forEach((obj) => { console.log(obj) })
- O(1)
◽️ 데이터가 얼마나 많든 상관없이 단계수가 일정한 경우에 쓴다.
◽️ 예를 들어, index로 바로 접근하는 경우가 있다.
const arr = [1, 2, 3]
console.log(arr[0]) // 1
- O(logN)
◽️ "빅 오 로그 N"이라고 발음한다.
◽️ 데이터가 두 배로 증가할 때 마다 한 단계씩 늘어나는 알고리즘을 설명한다. (log₂8=3, log₂64=6...)
◽️ 배열의 길이를 2로 나누어 가운데 셀의 인덱스를 구해 가운데부터 검색하는 이진검색이 대표적인 예시이다.
◽️ 컴퓨터 과학에서 O(logN)은 O(log₂N)을 줄여 부르는 방식이다.
Set vs. Array
1) Array의 빅 오
◽️ O(1) : push, pop
◽️ O(N logN) : sort
◽️ O(N) : shift, unshift, slice, splice, concat, forEach, map, filter, reduce...
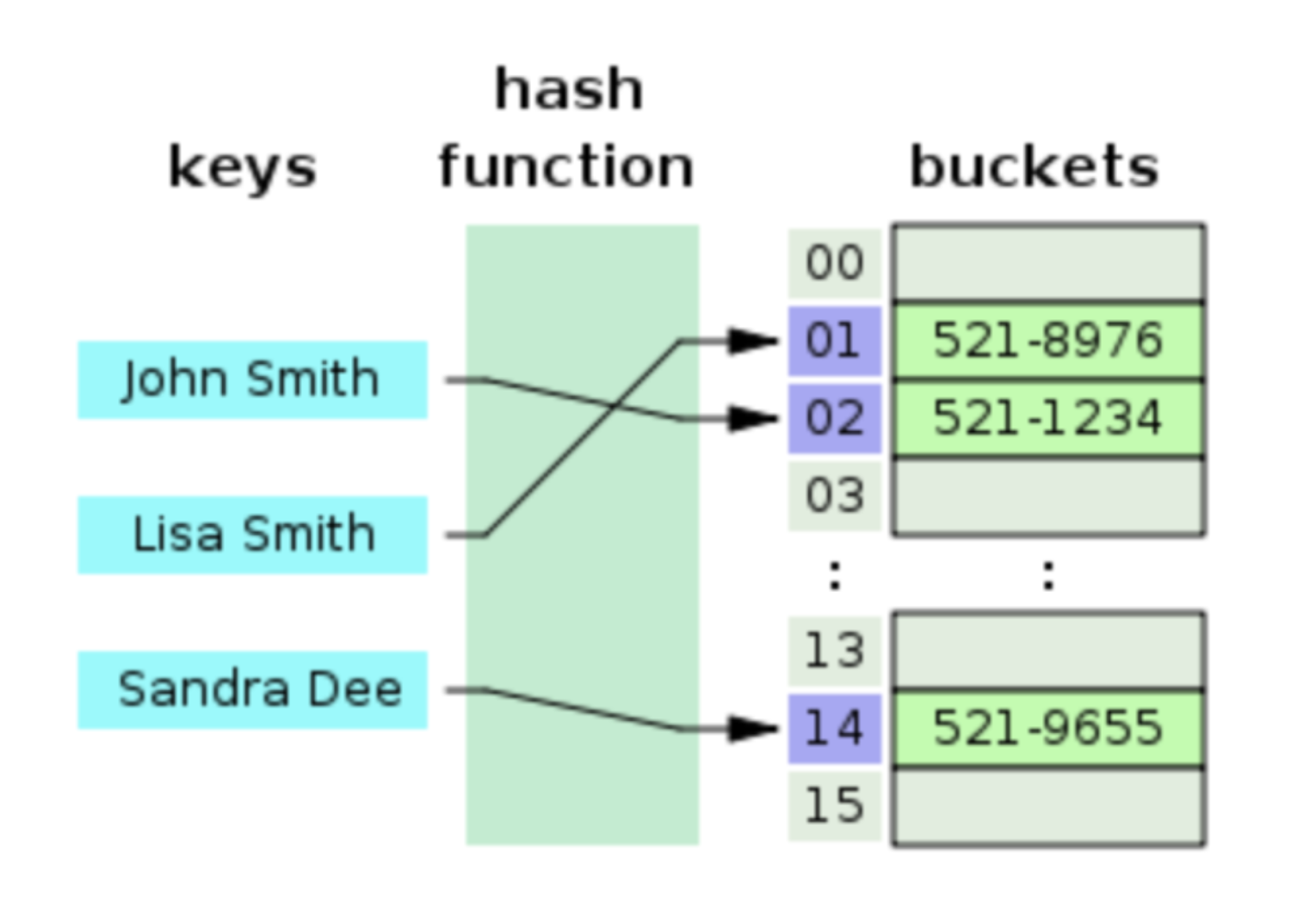
2. Set과의 비교
◽️ Set은 key, value로 데이터를 저장하는 해시테이블 자료구조를 갖고 있다. key값에 해시함수를 적용해 배열의 고유한 index를 생성하고 이 index를 활용하여 값을 저장하고 검색하기 때문에 검색속도가 빠르다.
◽️ 값을 추가할 때는 Array와 Set은 O(1)로 동일하나, 삽입/삭제 시에는 Array는 O(n), Set은 O(1)이다.
◽️ 작업 중 삭제, 삽입이 많은 경우 데이터 구조를 Set으로 변경하는 것도 좋은 방법이다.
알고리즘 개선하기
예시 1.
배열에서 중복된 숫자를 찾으면 boolean값을 리턴하는 함수를 작성해보자.
이중 루프를 사용하면 총 단계수는 25단계이며 시간복잡도가 O(N²)이 된다.
export const hasDuplicateValue = (array) => {
let steps = 0 // 단계의 수
for (let i = 0; i < array.length; i++) {
for (let j = 0; j < array.length; j++) {
steps++ // 단계수를 증가시킨다.
if(i !== j && array[i] === array[j]) {
return true
}
}
}
console.log('단계 수 >>> ', steps);
return false;
}
하지만 빈 배열의 찾는 값의 인덱스에 1이라는 값을 삽입하며 순회하는 로직으로 변경하면 총 단계수는 5단계로 O(N)이 되며, 기존보다 훨씬 빠른 알고리즘이 된다.
export const hasDuplicateValue = (array) => {
let steps = 0 // 단계의 수
let existingNumbers = []
for (let i = 0; i < array.length; i++) {
steps++ // 단계수를 증가시킨다.
if (existingNumbers[array[i]] === 1) {
return true
} else {
existingNumbers[array[i]] = 1
}
}
console.log('단계 수 >>> ', steps);
return false;
}
출처 및 참고
https://www.youtube.com/watch?v=xls6jEZNA7Y
누구나 자료구조와 알고리즘
'STUDY > 2024' 카테고리의 다른 글
| 📔 [스터디] 학습노트 - Stack, Queue (1) | 2024.01.13 |
|---|---|
| [스터디] 알고리즘: 3주차. Stack, Queue (0) | 2024.01.07 |
| 📔 [스터디] 학습노트 - 배열 (0) | 2024.01.02 |
| [스터디] 알고리즘: 2주차. 시간복잡도 (0) | 2023.12.29 |
| [스터디] 알고리즘: 1주차. 배열(Array) (0) | 2023.12.29 |




