| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 공통컴포넌트
- 타입좁히기
- 리액트
- 제네릭
- click and drag
- 폰트적용하기
- 레이아웃쪼개기
- NonNullable
- React.js
- 티스토리꾸미기
- 개발콘텐츠
- Chart.js
- utilty type
- 2022
- 타입스크립트
- returnType
- const 단언문
- 성능최적화
- react
- 커스텀
- 반복줄이기
- typescript
- TSDoc
- reactjs
- javascript
- 누구나 자료구조와 알고리즘
- CSS
- vue.js
- React Native
- JS console
- Today
- Total
몽땅뚝딱 개발자
⭐️ 누구나 자료구조와 알고리즘 - (12) 노드 기반 자료구조: 트리(Tree) - 힙(Heap), 트라이(trie) 본문
⭐️ 누구나 자료구조와 알고리즘 - (12) 노드 기반 자료구조: 트리(Tree) - 힙(Heap), 트라이(trie)
레오나르도 다빈츠 2023. 10. 1. 21:52

15장, 16장 다시 읽어보기 .. 🥺
트리(Tree)
순서를 유지하면서도 빠른 검색과 삽입, 삭제가 가능한 자료 구조가 필요한 경우에 사용한다. 트리도 노드 기반 자료 구조이지만 트리의 각 노드는 여러 노드로의 링크를 포함할 수 있다. 트리의 각 노드에는 다른 두 노드로 이어지는 링크가 있다.
1.1. 개념
- 루트(root): 가장 상위 노드로 꼭대기에 있다.
- 부모(parent), 자손(descendant), 조상(ancestor)
- 레벨(level): 각 줄을 의미한다.
- 프로퍼티(property): 균형 잡힌 정도이다. 모든 노드에서 하위 트리의 노드 개수가 같으면 그 트리는 균형(balanced) 트리다.
1.2 이진 탐색 트리

이진과 탐색이라는 수식어가 붙는데 이진 트리는 각 노드에 자식이 0개나 1, 2개이다.
- 각 노드의 자식은 최대 "왼쪽"에 하나, "오른쪽"에 하나다.
- 한 노드의 "왼쪽" 자손은 그 노드보다 작은 값만 포함할 수 있다. 한 노드의 "오른쪽" 자손은 그 노드보다 큰 값만 포함할 수 있다.
- 이진 탐색 트리로서 유효하려면 최대 왼쪽 자식 하나, 오른쪽 자식 하나만 있어야 한다.
1.3 이진 트리
1.3.1 검색
- 트리검색은 O(logN)이다. 레벨을 새로 추가할 때마다 트리 크기가 두 배가 되므로 노드가 N개면 레벨이 약 logN개이다.
- 검색할 노드의 개수를 반씩 줄여가며 검색한다.
1.3.2 삽입
- 이진 탐색 트리는 삽입에 가장 뛰어나다. 배열은 값을 삽입할 공간을 마련하기 위해 많은 데이터를 시프트하느라 삽입에 O(N)이 걸릴 수 있으나 이진 트리는 검색과 삽입 모두 O(logN)이다.
- 완벽한 선형으로 이루어진 트리는 O(N)이 소요된다. 따라서 정렬된 배열을 이진 탐색 트리로 변환하고 싶을 때는 먼저 데이터 순서를 무작위로 만드는게 좋다.
1.3.3 삭제
- 삭제 한 뒤 연결이 끊긴 트리는 삭제한 노드 자리에 넣는다.
- 자식이 둘 인 노드를 삭제할 경우, 삭제된 노드를 후속자 노드로 대체한다. 후속자 노드란 "삭제된 노드보다 큰 값 중 최솟값"을 갖는 자식 노드이다. 예를 들어, 56(부모)-52/61(자손)에서 56을 삭제하는 경우 61(부모)-52(자손)이 된다.
- 루트에 있는 값이 삭제되는 경우, 오른쪽 자식을 방문한 후 왼쪽 자식이 없는 노드가 나올 때 까지 계속 내려가 후속자 노드를 찾는다.
- 후속자 노드에 오른쪽 자식이 있는 경우 후속자 노드를 삭제된 자리에 넣고 후속자 노드의 오른쪽 자식을 원래 부모의 왼쪽 자식으로 넣는다.
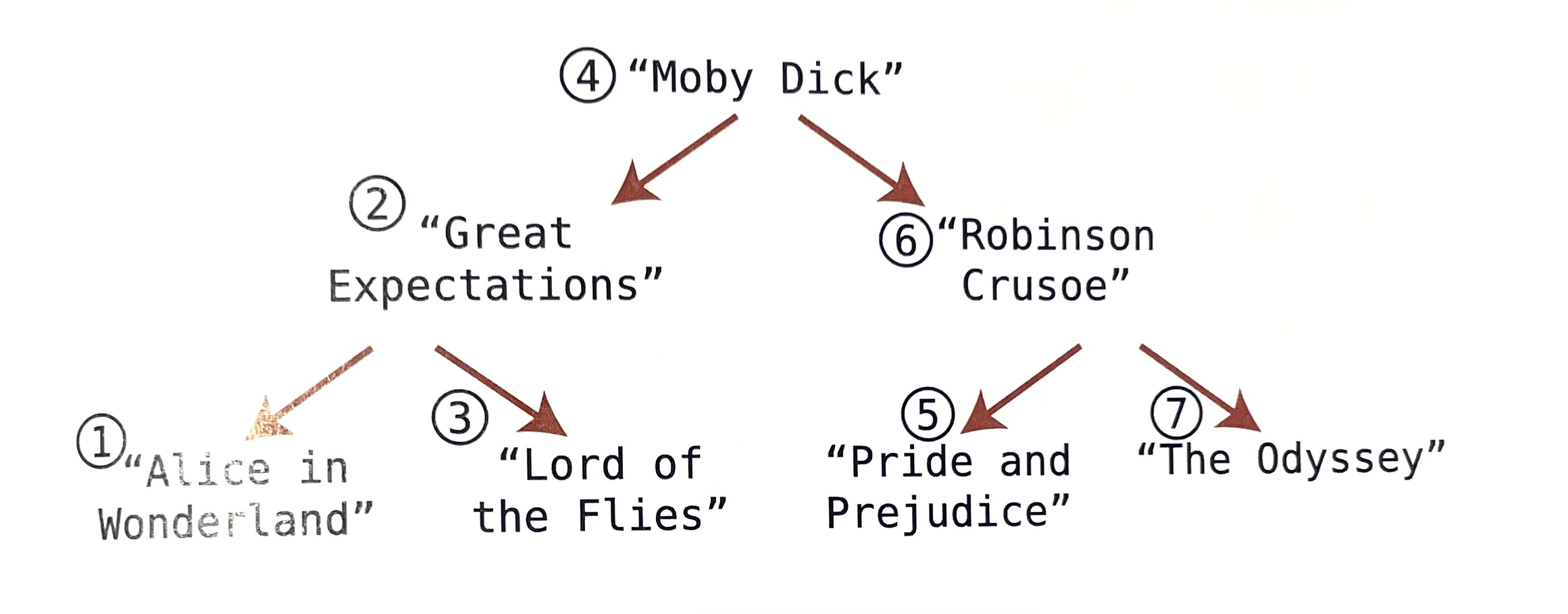
힙(heap)
트리의 자료구조 중에서 힙은 특수한 종류의 이진 트리로 데이터 세트에서 가장 크거나 작은 데이터 원소를 계속 알아내야 할 때 유리하다.
예를 들어, 우선순위 큐는 앞에서만 데이터에 접근하고 삭제하되 데이터를 삽입할 때는 데이터를 늘 특정 순서대로 정렬시킨다. 만약 우선순위 큐를 배열로 구현할 시에는 삭제 시 O(1)이지만 삽입 시에는 O(N)의 효율성이다.
우선순위 큐를 구현할 때 효율적으로 쓰이는 자료구조가 바로 힙(heap)이다.
1.1. 이진 힙(binary heap)
이진 힙(binary heap)은 힙의 많은 종류 중 하나이다. 특징은 아래와 같다.
- 최대 힙과 최소 힙이라는 두 종류가 있다.
- 힙 조건(heap condition): 각 노드의 값은 그 노드의 모든 자손 노드의 값보다 커야 한다.
- 완전 트리(complete tree): 트리는 완전해야 한다.
- 완전 트리는 빠진 노드 없이 노드가 완전히 채워진 트리로 트리의 각 레벨의 모든 자리마다 노드가 있다.
- 바닥 줄에는 빈 자리가 있을 수 있다.
- 빈 자리의 오른쪽으로 어떤 노드도 없어야 한다.
- 대 힙은 루트 노트를 기준으로 레벨이 내려갈 수록 부모보다 큰 값은 없으며, 최소 힙은 그 반대이다.
1.2 힙의 속성
1.2.1 삽입
새 값을 포함하는 노드를 생성하고 바닥 레벨의 가장 오른쪽 노드 옆에 삽입한다. 삽입한 노드와 그 부모 노드를 비교하면서 새 노드보다 큰 노드를 만날 때 까지 3단계를 반복하며 새 노드를 힙 위로 올린다. 올리는 과정을 노드를 위로 트리클링(trickling)한다고 표현한다.
1.2.2 삭제
힙에서 값을 삭제하려면 루트 노드만 삭제할 수 있다. 마지막 노드를 루트에 덮어쓰고 루트와 자손을 아래로 트리클링하며 비교한 뒤 값을 스왑한다.
1.3 힙 vs. 정렬된 배열
| 정렬된 배열 | 힙 | |
| 삽입 | O(N) | O(logN) |
| 삭제 | O(1) | O(logN) |
정렬된 배열은 삽입에 있어 힙보다 느리지만 삭제는 힙보다 빠르다. 우선순위 큐를 구현할 때 O(1)이 엄청나게 빠르긴 해도 O(logN) 역시 빠르므로 힙을 선택하는 것이 낫다.
1.3.1 배열 기반 힙
배열 기반 힙 순회 시 아래와 같은 특성이 있다.
- 어떤 노드의 왼쪽 자식을 찾으려면 (index * 2) + 1 공식을 사용한다.
- 어떤 노드의 오른쪽 자식을 찾으려면 (index * 2) + 2 공식을 사용한다.
- 어떤 노드의 부모를 찾으려면 (index - 1) / 2 공식을 사용한다.
트라이(trie)
트리의 자료구조 중에서 트라이는 자동 완성 같은 텍스트 기반 기능에 이상적이다. 대부분의 트리처럼 트라이도 다른 노드를 가리키는 노드들의 컬렉션이다. 이진 트리는 노드에 셋 이상의 자식이 있을 수 없으나 트라이 노드는 자식 노드 개수에 제한이 없다.
1.1 검색
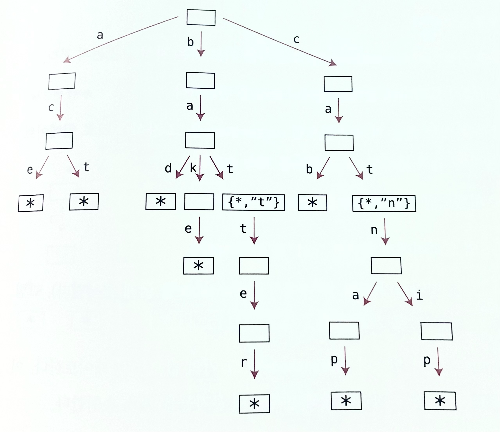
- 이진 검색이 O(logN)이 소요된다면 트라이 검색은 검색 시 문자열 만큼 단계가 걸린다. 빅오로 나타낼 때는 O(K)로 나타내며 K는 문자열의 수를 의미한다.
1.2 삽입
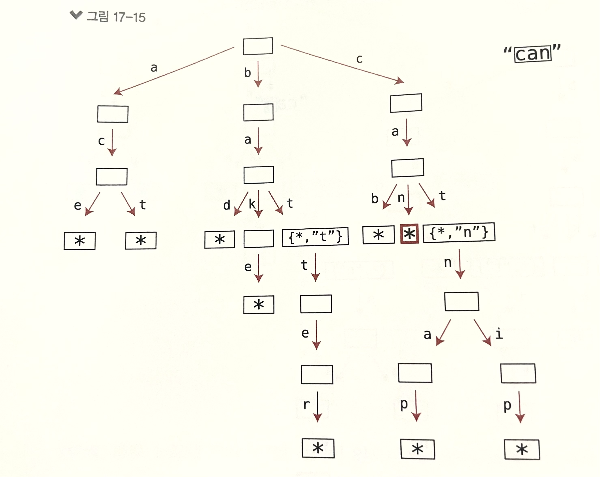
출처
제이 웹그로우, 누구나 자료구조와 알고리즘 (길벗, 2021)
개인적으로 공부한 내용을 정리하는 블로그로
잘못된 개념을 게시하지않도록 주의하고 있으나 오류가 있을 수 있습니다.
'Development > 알고리즘' 카테고리의 다른 글
| 누구나 자료구조와 알고리즘 - (14) 공간 제약 다루기, 코드 최적화 기법 (0) | 2023.10.03 |
|---|---|
| 누구나 자료구조와 알고리즘 - (13) 그래프 (0) | 2023.10.03 |
| 누구나 자료구조와 알고리즘 - (11) 노드 기반 자료구조: 연결 리스트 (0) | 2023.09.29 |
| 누구나 자료구조와 알고리즘 - (10) 퀵 정렬(Quicksort) (0) | 2023.09.29 |
| 누구나 자료구조와 알고리즘 - (9) 재귀 (0) | 2023.09.28 |




